Chapitre XI : Détection et gestion des collisions avec SDL

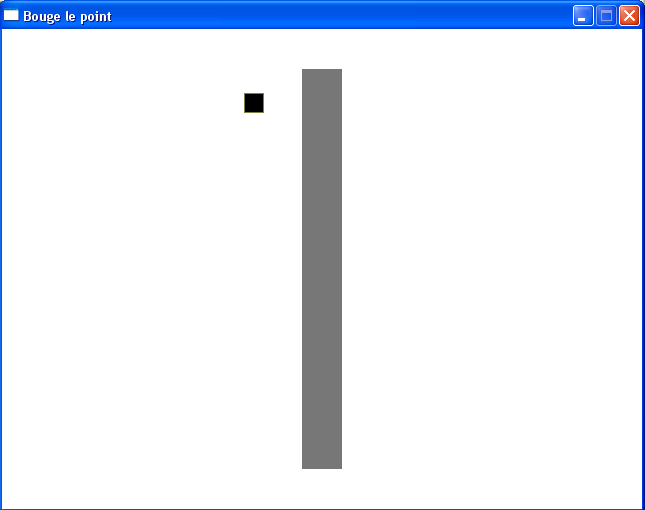
Pour cette première partie, nous avons donc un carré et un mur. Il va falloir qu'on fasse en sorte que le carré ne traverse pas le mur.
Voici à quoi ressemblera notre premier programme :

Pour ce faire, il nous faut vérifier si le carré et le mur sont en collision.

Construisons d'abord notre mur et notre carré :

//Le mur
SDL_Rect wall;

//La classe Square (carre)
class Square
{
    private:
    //la boite de collision du carre
    SDL_Rect box;
 
    //La vitesse du point
    int xVel, yVel;
 
    public:
    //Initialisation des variables
    Square();
 
    //Recupere la touche pressee et ajuste la vitesse du carre
    void handle_input();
 
    //Montre le carré sur l'ecran
    void show();
};

La classe Square représente le carré qu'on va déplacer dans la fenêtre SDL.
Comme vous pouvez le remarquer, cette classe est quasi-identique à notre classe Point vue dans les chapitres précédents.
La seule différence notable est que les coordonnées X et Y de notre carré sont dans une structure SDL_Rect qui contient aussi les dimensions de notre carré.

Nous avons donc deux SDL_Rect et il nous faut déterminer quand il y a collision.
La fonction suivante va prendre en paramètre nos deux SDL_Rect, calculer les côtés de nos rectangles (le carré et le mur) afin d'ensuite faire les tests de collision.

bool check_collision( SDL_Rect &A, SDL_Rect &B )
{
    //Les cotes des rectangles
    int leftA, leftB;
    int rightA, rightB;
    int topA, topB;
    int bottomA, bottomB;
 
    //Calcul les cotes du rectangle A
    leftA = A.x;
    rightA = A.x + A.w;
    topA = A.y;
    bottomA = A.y + A.h;
 
    //Calcul les cotes du rectangle B
    leftB = B.x;
    rightB = B.x + B.w;
    topB = B.y;
    bottomB = B.y + B.h;

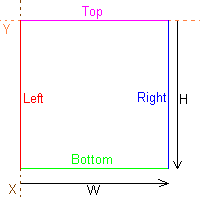
Comme vous le voyez, il est facile à partir d'un SDL_Rect de calculer les côtés des rectangles car nous possédons ses coordonnées X et Y ainsi que sa hauteur H et sa largeur W.

Si vous avez du mal à voir comment les côtés sont déterminés, voici un petit schéma :

Maintenant que nous avons ce qu'il nous faut, nous pouvons tester si les deux rectangles sont en collision.
Il existe des cas, faciles à déterminer, où la collision entre les deux rectangles est impossible :
cas 1 - La partie basse (bottom) du rectangle A se retrouve au-dessus de la partie haute (Top) du rectangle B.
cas 2 - La partie haute (Top) du rectangle A se retrouve en dessous de la partie basse (bottom) du rectangle B.
cas 3 - La partie gauche (Left) du rectangle A se retrouve plus à droite que la partie droite (Right) du rectangle B.
cas 4 - La partie droite (Right) du rectangle A se retrouve plus à gauche que la partie gauche (Left) du rectangle B.

Un schéma valant mieux qu'une explication :

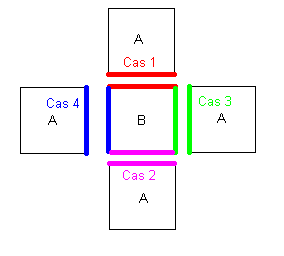
Dans les autres cas, il y a collision.
Il est donc facile de vérifier s'il y a collision entre nos deux rectangles, il suffit de vérifier qu'ils ne sont pas dans l'un des quatre cas présentés ci-dessus.

    //Tests de collision
    if( bottomA <= topB )
    {
        return false;
    }
 
    if( topA >= bottomB )
    {
        return false;
    }
 
    if( rightA <= leftB )
    {
        return false;
    }
 
    if( leftA >= rightB )
    {
        return false;
    }
 
    //Si conditions collision detectee
    return true;
}

Notez que j'ai utilisé les opérateurs égal dans les tests, j'ai juste décidé qu'il n'y avait pas collision lorsque les deux rectangles étaient collés.
Vous pouvez très bien enlever les opérateurs égal, dans ce cas quand les deux rectangles seront côte à côte, il y aura collision (ce qui peut poser problème, nous le verrons par la suite).

Continuons ce programme par l'affichage du carré.
C'est dans cette fonction d'affichage et de rendu que l'on va utiliser notre fonction de collision et faire le traitement le cas échéant.

void Square::show() {
    //Bouge le carre a droite ou a gauche
    box.x += xVel;
 
    //Si collision avec les cotes de l'ecran (droite ou gauche) ou collision avec le mur
    if( ( box.x < 0 ) || ( box.x + SQUARE_WIDTH > SCREEN_WIDTH ) || ( check_collision( box, wall ) ) ) {
        //Annulation du dernier deplacement
        box.x -= xVel;
    }
 
    //Bouge le carre vers le haut ou vers le bas
    box.y += yVel;
    //Si collision avec les cotes de l'ecran (haut ou bas) ou collision avec le mur
    if( ( box.y < 0 ) || ( box.y + SQUARE_HEIGHT > SCREEN_HEIGHT ) || ( check_collision( box, wall ) ) ) {
        //Annulation du dernier deplacement
        box.y -= yVel;
    }
    //Affiche le carre
    apply_surface( box.x, box.y, square, screen );
}

Dans cette fonction, nous bougeons notre carré.
Nous vérifions que celui-ci ne sort pas de l'écran ou qu'il ne traverse pas le mur.
Si notre carré est en collision, que ce soit avec les bords de l'écran ou avec notre mur, on annule le déplacement.
L'algorithme utilisé est donc celui-ci :

On bouge le carre
Si il y a une collision dans cette nouvelle position
    On annule le mouvement
Fin Si

Un petit problème peut apparaître selon la taille de notre fenêtre SDL et la vitesse de déplacement de notre carré.
En effet, si ces trois valeurs (hauteur de l'écran, largeur de l'écran et vitesse de déplacement du carré), ne sont pas multiples, il peut y avoir un problème de ce type :

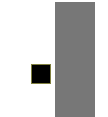
Comme vous pouvez le voir, le carré reste bloqué sans pouvoir se coller au mur, ce qui n'est pas très réaliste comme collision.
Pour combler ce défaut, nous allons utiliser un autre algorithme :

On bouge le carré
Si il y a une collision dans cette nouvelle position
    On colle le carré contre l'élément en collision
Fin Si

Cet algorithme est préférable au premier lors de collisions avec des éléments statiques mais à éviter dans le cas de collisions avec des éléments dynamiques.
Voici donc une autre version de la fonction d'affichage du carré :

void Square::show()
{
    //Bouge le carre a droite ou a gauche
    box.x += xVel;
 
    int leftW, leftB;
    int rightW, rightB;
    int topW, topB;
    int bottomW, bottomB;
 
    leftB = box.x;
    rightB = box.x + box.w;
    topB = box.y;
    bottomB = box.y + box.h;
 
    leftW = wall.x;
    rightW = wall.x + wall.w;
    topW = wall.y;
    bottomW = wall.y + wall.h;
 
    //Si collision avec les cotes de l'ecran (droite ou gauche)
    if( ( box.x < 0 ) ) {
        //On colle le carre contre l'ecran
        box.x = 0;
    }
    if ( box.x + SQUARE_WIDTH > SCREEN_WIDTH ) {
        //On colle le carre contre l'ecran
        box.x = SCREEN_WIDTH - SQUARE_WIDTH;
    }
    //Si collision avec le mur
    if( ( check_collision( box, wall )) ) {
        // collision droite
        if(box.x + box.w > wall.x + wall.w) {
            box.x = wall.x + wall.w;
        }
        // collision gauche
        if(box.x < wall.x) {
            box.x = wall.x - box.w;
        }
    }
 
    //Bouge le carre vers le haut ou vers le bas
    box.y += yVel;
 
    //Si collision avec les cotes de l'ecran (haut ou bas)
    if( ( box.y < 0 ) ) {
        //On colle le carre contre l'ecran
        box.y = 0;
    }
    if ( box.y + SQUARE_HEIGHT > SCREEN_HEIGHT ) {
        //On colle le carre contre l'ecran
        box.y = SCREEN_HEIGHT - SQUARE_HEIGHT;
    }
    //Si collision avec le mur
    if( ( check_collision( box, wall )) ) {
        // collision haut
        if(box.y < wall.y){
            box.y = wall.y - box.h;
        }
 
        // collision bas
        if(box.y + box.h > wall.y + wall.h) {
            box.y = wall.y + wall.h;
        }
    }
 
    //Affiche le carre
    apply_surface( box.x, box.y, square, screen );
}

Cette version est plus lourde que la précédente car il nous faut récupérer les côtés de nos deux rectangles afin de pouvoir les coller lors d'une collision.
Dans le cas où nous aurions mis un opérateur égal dans les tests de collision dans notre fonction check_collision plus haut, il y aurait eu une boucle infinie entre la détection de la collision et le placement du carré.

Enfin pour terminer cette fonction, on affiche bien sûr le carré à l'écran.

Les sources de ce programme sont téléchargeables ici :
Télécharger les sources du chapitre XI-1 version 1 (100 ko)
Télécharger les sources du chapitre XI-1 version 2 (101 ko)

Une des méthodes les plus utilisées dans le monde du jeu vidéo est la gestion des collisions avec des boîtes de collision.
Cette partie du tutoriel va vous apprendre à créer et utiliser ces boîtes afin de détecter les collisions.

Avec les boîtes de collision, vous pouvez vérifier les collisions pour n'importe quel type de figure géométrique car tout peut se rapporter à un ensemble de boîtes de collision.
Prenons l'exemple d'un point :

Celui-ci peut se représenter avec un ensemble de boîtes de collision comme celles-ci :

Chaque image sur un ordinateur est composée de pixels, et les pixels sont des carrés qui composent des rectangles qui seront nos boîtes de collision.
Ainsi, lorsque l'on souhaite vérifier une collision, il suffit de vérifier si les deux groupes de rectangles entrent en collision.

Pour gérer ces groupes de rectangle qui nous servirons de boîtes de collision, nous allons utiliser des vecteurs.

#include "SDL/SDL.h"
#include "SDL/SDL_image.h"
#include <string>
#include <vector>

Les vecteurs sont des sortes de tableaux, mais sont plus facile à gérer. Si vous ne connaissez pas, je vous conseille d'aller ici :
FAQ vector

Nous allons devoir revoir un peu la classe Point que nous avions définie dans les chapitres précédents car il va nous falloir ajouter les boîtes de collision.

//La classe Point
class Point
{
    private:
    //Les coordonnees du point
    int x, y;
 
    //Les boites de collision du point
    std::vector<SDL_Rect> box;
 
    //La velocite du point
    int xVel, yVel;
 
    //fonction pour les boites de collision
    void shift_boxes();
 
    public:
    //Initialisation des variables
    Point( int X, int Y );
 
    //Prend les touches pressees et ajuste la vélocite du point
    void handle_input();
 
    //Bouge le point
    void move( std::vector<SDL_Rect> &rects );
 
    //Montre le point à l'écran
    void show();
 
    //Recuperation des boites de collision
    std::vector<SDL_Rect> &get_rects();
};

Nous avons les coordonnées et la vélocité du point comme avant, mais maintenant on a en plus un vecteur de SDL_Rect pour contenir les boîtes de collision.

Au niveau des fonctions, on voit apparaître la fonction shift_boxes() qui bouge les boîtes de collision en relation avec les coordonnées.

Il y a aussi un constructeur qui initialise le Point aux coordonnées passées en paramètre ainsi que la fonction de récupération des événements déjà présente avant.
Cette fois-ci on va séparer la partie mouvement du Point de la partie affichage de celui-ci.
Nous avons aussi une fonction get_rects() qui va nous permettre de récupérer les boîtes de collision.

Passons à la fonction de vérification des collisions.
Cette fois-ci on ne va pas se contenter de vérifier la collision entre deux rectangles, mais entre deux groupes de rectangles qui sont nos boîtes de collisions de nos deux éléments.

bool check_collision( std::vector<SDL_Rect> &A, std::vector<SDL_Rect> &B )
{
    //Les cotes du rectangle
    int leftA, leftB;
    int rightA, rightB;
    int topA, topB;
    int bottomA, bottomB;
 
    //On va dans la boite A
    for( int Abox = 0; Abox < A.size(); Abox++ )
    {
        //Calcul des cotes du rectangle A
        leftA = A[ Abox ].x;
        rightA = A[ Abox ].x + A[ Abox ].w;
        topA = A[ Abox ].y;
        bottomA = A[ Abox ].y + A[ Abox ].h;
 
        //On va dans la boite B
        for( int Bbox = 0; Bbox < B.size(); Bbox++ )
        {
            //Calcul des cotes du rectangle B
            leftB = B[ Bbox ].x;
            rightB = B[ Bbox ].x + B[ Bbox ].w;
            topB = B[ Bbox ].y;
            bottomB = B[ Bbox ].y + B[ Bbox ].h;
 
            //Si les cotes de A sont en dehors de B
            if( ( ( bottomA <= topB ) || ( topA >= bottomB ) || ( rightA <= leftB ) || ( leftA >= rightB ) ) == false )
            {
                //Une collision est detectee
                return true;
            }
        }
    }
 
    //Si aucune des boites de collision ne se touchent
    return false;
}

Cette fonction prend un rectangle du vecteur A, puis vérifie s'il y a collision avec tous les rectangles du vecteur B, ensuite on prend le rectangle A suivant et on recommence l'opération.
Ce travail est effectué jusqu'à ce qu'on trouve une collision ou qu'on ait testé tous les rectangles ensemble.

Nous allons maintenant nous occuper de la création de notre point et de ses boîtes de collision.

Point::Point( int X, int Y )
{
    //Initialisation des coordonnées
    x = X;
    y = Y;
 
    //Initialisation de la velocite
    xVel = 0;
    yVel = 0;
 
    //Creation des SDL_Rects necessaires
    box.resize( 11 );
 
    //Initialisation des hauteurs et largeurs des boites de collision
    box[ 0 ].w = 6;
    box[ 0 ].h = 1;
 
    box[ 1 ].w = 10;
    box[ 1 ].h = 1;
 
    box[ 2 ].w = 14;
    box[ 2 ].h = 1;
 
    box[ 3 ].w = 16;
    box[ 3 ].h = 2;
 
    box[ 4 ].w = 18;
    box[ 4 ].h = 2;
 
    box[ 5 ].w = 20;
    box[ 5 ].h = 6;
 
    box[ 6 ].w = 18;
    box[ 6 ].h = 2;
 
    box[ 7 ].w = 16;
    box[ 7 ].h = 2;
 
    box[ 8 ].w = 14;
    box[ 8 ].h = 1;
 
    box[ 9 ].w = 10;
    box[ 9 ].h = 1;
 
    box[ 10 ].w = 6;
    box[ 10 ].h = 1;
 
    //On bouge les boites de collision
    shift_boxes();
}

On met le point aux coordonnées données en argument et on initialise sa vélocité.
Ensuite nous créons onze boîtes de collision dans le vecteur dont nous initialisons la largeur et la hauteur.
Il nous faut ensuite les disposer comme sur l'image du point plus haut (rectangles noirs et bleus).

Cette dernière chose est faite grâce à la fonction shift_boxes() :

void Point::shift_boxes()
{
    //Initialisation
    int r = 0;
 
    //On va dans les boites de collision du point
    for( int set = 0; set < box.size(); set++ )
    {
        //On centre la boite de collision
        box[ set ].x = x + ( POINT_WIDTH - box[ set ].w ) / 2;
 
        //On met la boite de collision à sa place
        box[ set ].y = y + r;
 
        //On bouge la position en dessous de la hauteur de la boite de collision
        r += box[ set ].h;
    }
}

Cette fonction va placer nos boîtes de collision sur le point et faire en sorte que si on bouge notre point, les boîtes de collision le suivront disposées de la même façon.
Pour mieux comprendre cette fonction, je vous conseille de la faire tourner sur un papier par exemple.

Nous allons nous occuper du mouvement de notre point et faire le nécessaire lors de collisions, tout ceci dans la fonction move().

void Point::move( std::vector<SDL_Rect> &rects )
{
    //Bouge le point a droite ou a gauche
    x += xVel;
 
    //Bouge la boite de collision
    shift_boxes();
 
    //Si le point a ete trop loin a droite ou a gauche ou est en collision avec un autre objet
    if( ( x < 0 ) || ( x + POINT_WIDTH > SCREEN_WIDTH ) || ( check_collision( box, rects ) ) )
    {
        //On revient en arriere (annulation du mouvement)
        x -= xVel;
        shift_boxes();
    }
 
    //Bouge le point vers le haut ou le bas
    y += yVel;
 
    //Bouge la boite de collision
    shift_boxes();
 
    //Si le point a ete trop loin a droite ou a gauche ou est en collision avec un autre objet
    if( ( y < 0 ) || ( y + POINT_HEIGHT > SCREEN_HEIGHT ) || ( check_collision( box, rects ) ) )
    {
        //On revient en arriere (annulation du mouvement)
        y -= yVel;
        shift_boxes();
    }
}

C'est à peu près la même chose qu'avant.
Nous bougeons le point, et si le point va en dehors de l'écran ou qu'une collision est détectée entre deux groupes de rectangles, on annule le mouvement.
La seule différence réside dans le déplacement des boîtes de collision avec le point avec la fonction shift_boxes().

Il nous manque aussi l'affichage du point que voici :

void Point::show()
{
    //Affiche le point
    apply_surface( x, y, point, screen );
}

J'ai volontairement porté l'utilisation des boîtes de collision à outrance pour montrer qu'on peut faire des collisions "pixel-perfect" (au pixel près) en les utilisant.
Cependant, il n'est pas nécessaire d'en faire autant pour créer des collisions réalistes et la plupart des jeux vidéos utilisent des boîtes de collision grossières loin du pixel avec beaucoup moins de précision.
La précision au pixel est rarement nécessaire pour faire quelque chose de réaliste, c'est à vous de décider de la précision que vous souhaitez.

Les sources de cette partie du tutoriel sont disponibles ici : Télécharger les sources du chapitre XI-2 (106 ko)

Dans la partie précédente, nous avons utilisé onze boîtes de collision pour un cercle (notre point).
Dans cette partie, on va apprendre une méthode plus efficace pour gérer la détection des collisions avec des cercles.

Nous allons avoir besoin d'un peu de math cette fois-ci, donc nous allons inclure une librairie supplémentaire, la librairie cmath.

//Les fichiers d'entete
#include <SDL/SDL.h>
#include <SDL/SDL_image.h>
#include <string>
#include <vector>
#include <cmath>

Nous allons aussi devoir créer notre propre structure de cercle pour ce programme :

//Une structure cercle
struct Circle
{
    int x, y;
    int r;
};

Les variables x et y sont les coordonnées du cercle et r est le rayon.

Nous allons une fois de plus revoir notre classe Point :

///La classe Point
class Point
{
    private:
    //La zone du point
    Circle c;
 
    //La velocite du point
    int xVel, yVel;
 
    public:
    //Initialisation des variables
    Point();
 
    //Prend les touches pressees et ajuste la velocite du point
    void handle_input();
 
    //Bouge le point
    void move( std::vector<SDL_Rect> &rects, Circle &circle );
 
    //Montre le point à l'ecran
    void show();
};

Nous avons deux différences par rapport à avant : cette fois nous utilisons notre structure cercle au lieu d'un vecteur de SDL_Rect et dans la fonction move() nous vérifions la collision entre un cercle et un vecteur de SDL_Rect.

Pour vérifier les collisions, nous allons avoir besoin de quelque chose en plus : connaître la distance entre deux points :

double distance( int x1, int y1, int x2, int y2 )
{
    //Retourne la distance entre deux points
    return sqrt( pow( x2 - x1, 2 ) + pow( y2 - y1, 2 ) );
}

Je ne pense pas avoir à expliquer cette formule, il s'agit simplement de mathématiques.

Nous allons utiliser deux fonctions pour vérifier les collisions, une entre deux cercles et l'autre entre un cercle et un vecteur de rectangles.
Vérifier les collisions entre deux cercles est assez simple, tout ce qu'on a à faire c'est de vérifier si oui ou non la distance entre les centres des deux cercles est inférieure à la somme de leurs rayons :

bool check_collision( Circle &A, Circle &B )
{
    //Si la distance entre le centre des cercles est inferieure à la somme de leurs radian
    if( distance( A.x, A.y, B.x, B.y ) < ( A.r + B.r ) )
    {
        //Le cercle est en collision
        return true;
    }
 
    //S'il ne l'est pas
    return false;
}

La fonction de vérification des collisions entre un cercle et un groupe de rectangles est un peu plus complexe.
Il y a deux types de collision possibles comme montrés sur cette image:

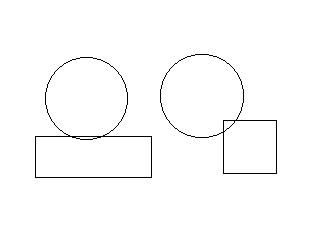
Le cercle peut toucher un côté ou un coin du rectangle.
Donc nous avons à prendre en compte les côtés du rectangle, les "côtés" du cercle et les coins du rectangle.
Pour calculer les "côtés" du cercle, nous allons utiliser son rayon et déterminer deux segments qui nous serviront de base pour les collisions comme sur l'image suivante :

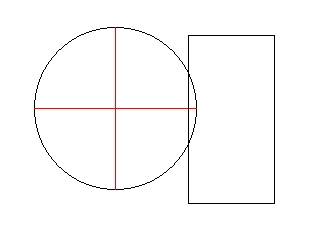
Voici le code permettant de déterminer ses "côtés" :

    //Calcul des cotes de A
    leftAv = A.x;
    rightAv = A.x;
    topAv = A.y - A.r;
    bottomAv = A.y + A.r;
 
    leftAh = A.x - A.r;
    rightAh = A.x + A.r;
    topAh = A.y;
    bottomAh = A.y;

Les quatre premières lignes définissent le "côté" vertical, les quatre suivantes le "côté" horizontal du cercle.

Ainsi quand nous vérifions les collisions avec les côtés du cercle, nous vérifions s'il y a collision entre les rectangles et les lignes formant les deux côtés du cercle.

Une ligne est juste un rectangle avec une épaisseur de un, donc la vérification de collision est la même qu'avant.

    //On va dans la boite B
    for( int Bbox = 0; Bbox < B.size(); Bbox++ )
    {
        //Calcul des cotes de B
        leftB = B[ Bbox ].x;
        rightB = B[ Bbox ].x + B[ Bbox ].w;
        topB = B[ Bbox ].y;
        bottomB = B[ Bbox ].y + B[ Bbox ].h;
 
        //Calcul des angles de B
        Bx1 = B[ Bbox ].x, By1 = B[ Bbox ].y;
        Bx2 = B[ Bbox ].x + B[ Bbox ].w, By2 = B[ Bbox ].y;
        Bx3 = B[ Bbox ].x, By3 = B[ Bbox ].y + B[ Bbox ].h;
        Bx4 = B[ Bbox ].x + B[ Bbox ].w, By4 = B[ Bbox ].y + B[ Bbox ].h;
 
        //Si aucun cote de la verticale A est en dehors de B
        if( ( ( bottomAv <= topB ) || ( topAv >= bottomB ) || ( rightAv <= leftB ) || ( leftAv >= rightB ) ) == false )
        {
            //Une collision est detectee
            return true;
        }
 
        //Si aucun cote de l'horizontale A est en dehors de B
        if( ( ( bottomAh <= topB ) || ( topAh >= bottomB ) || ( rightAh <= leftB ) || ( leftAh >= rightB ) ) == false )
        {
            //Une collision est detectee
            return true;
        }

Nous calculons les côtés et les angles des rectangles de la boîte B.
Ensuite on vérifie la collision rectangle-rectangle comme vue dans les parties précédentes.
La partie qu'il nous reste est la vérification des collisions avec les coins des rectangles.

        //Si un des coins de B est dans A
        if( ( distance( A.x, A.y, Bx1, By1 ) < A.r ) || ( distance( A.x, A.y, Bx2, By2 ) < A.r ) || ( distance( A.x, A.y, Bx3, By3 ) < A.r ) || ( distance( A.x, A.y, Bx4, By4 ) < A.r ) )
        {
            //Une collision est detectee
            return true;
        }
    }
 
    //Pas de collision
    return false;
}

Pour cela on regarde si les coins se trouvent à l'intérieur du cercle tout simplement.

A la fin, s'il n'y a pas eu de collisions, la fonction retourne faux.

Les sources de cette partie du tutoriel peuvent être récupérées ici :
Télécharger les sources du chapitre XI-3 (107 ko)

Télécharger les sources du chapitre XI-1 version 1 (100 ko)
Télécharger les sources du chapitre XI-1 version 2 (101 ko)
Télécharger les sources du chapitre XI-2 (106 ko)
Télécharger les sources du chapitre XI-3 (107 ko)

Version pdf (141 ko - 21 pages)